This research focus on a stochastic model predictive controller used for autonomous driving.

Particularly looks at the feedback loop generated when Ego-vehicles interacts with other playes in the environments and what would be a proper way to leverage on this interaction / feedback loop.

The controller factors in the uncertainty of two levels:

  1. Behavior Type
  2. Quantitative characterization of behavior.

The uncertainties were factored in through the chance constraints in stochastic model predictive control, and not part of the goal function as safety constraints need to be met hard.

++u_\tau = \arg \min_{u \in U} \sum_{t=\tau}^{\tau + T} l(x_t, u_t, c_t) + l_f(x_{\tau + T})++

++\text{for } \tau \in \mathcal{T}\text{, subject to } x_0 = x(t_0)++

++x_{n} = f(x_{n-1}, u_{n-1}) \text{ (Vehicle Dynamics)}++

++\text{For } || x_t - p_t || = d_t++

++ c_n = f_p(d_n | s) p(s)++

Where $s$ denotes the type of behavior of interacting vehicle and $f_p$ is the gaussian probability function for estimating probability of safety constraint violation:

++ \sigma^2 = A\Sigma^xA^T ++

$\sigma$ is used to determine the overlap of distribution to determine the probability of ego vehicle and target vehicle collinsion (prob. distribution overlap.)

$p(s)$ are randomly initialized and are sampled and updated via rolling window cumulative error:

++p(s)_{\tau} = (1-\alpha)p(s)_{\tau-1} + \alpha (1 - \frac{SSE_{t-1}(s)}{\sum(SSE_{t-1})})++

where

++SSE_\tau = SSE_{\tau-1} + \alpha \sum_{t = \tau - L}^{\tau - 1} ({\bar{x}_{tv, t}} - x_{tv, t})++

The end results are shown in this following GIF.

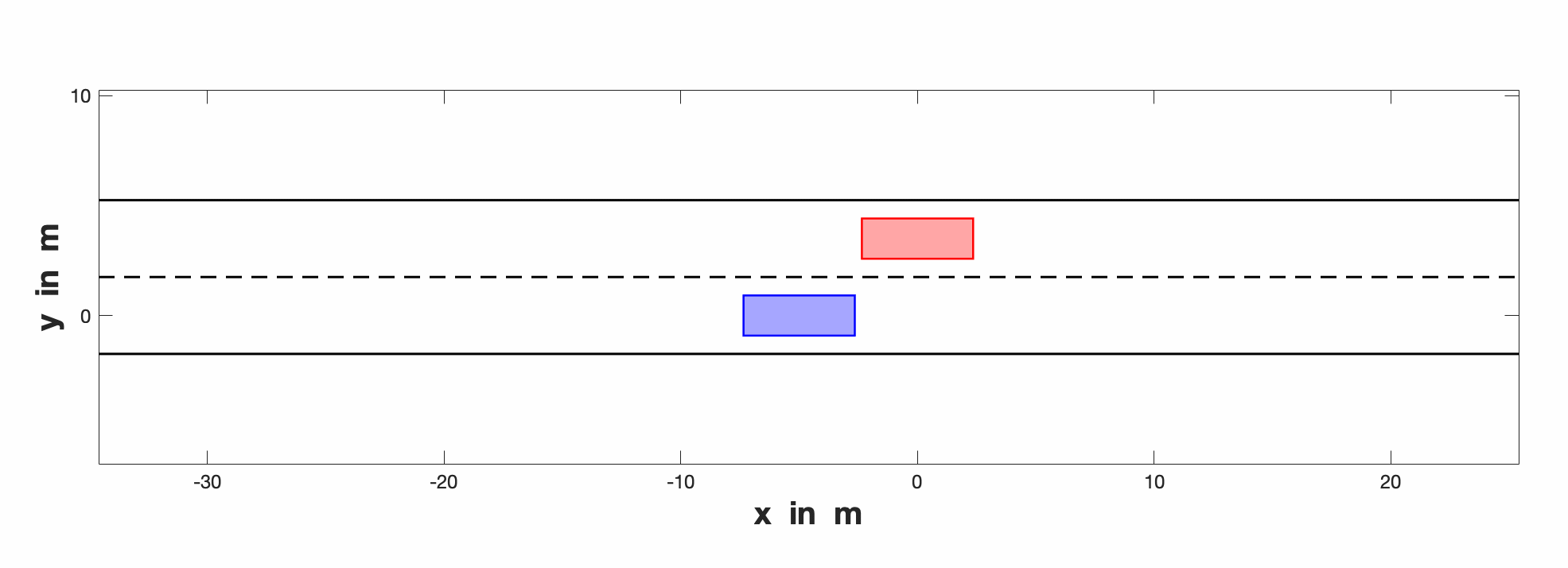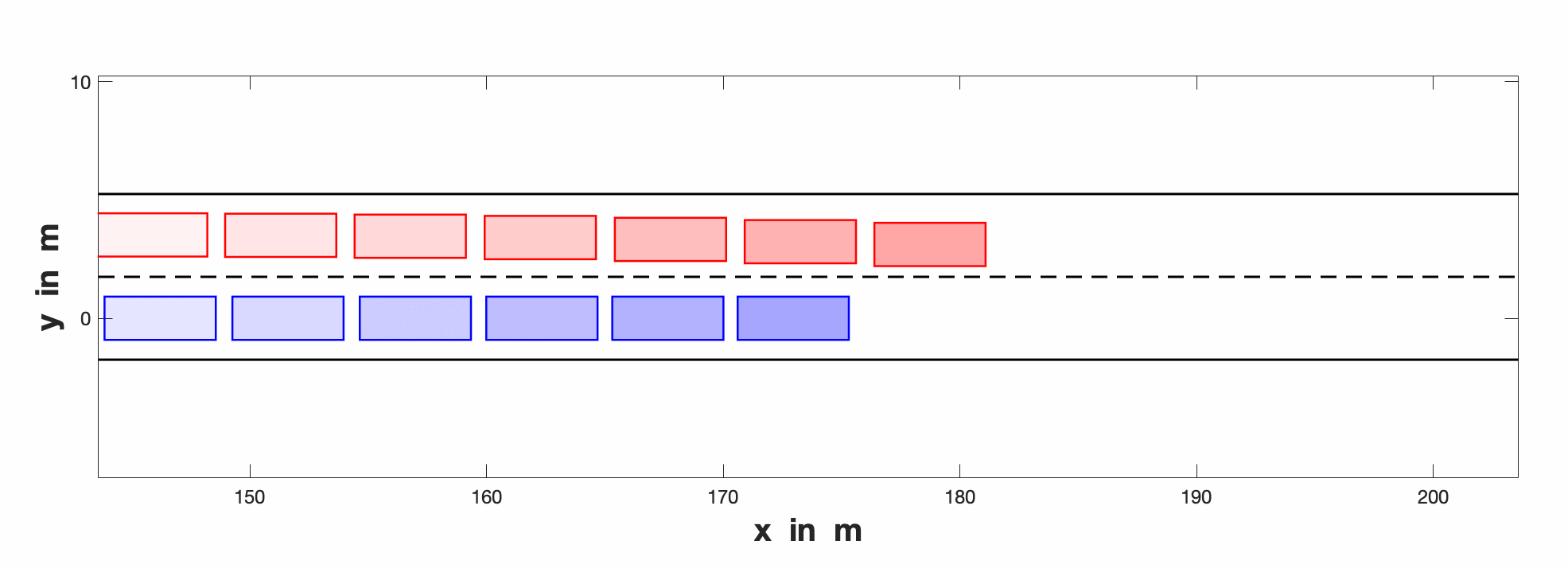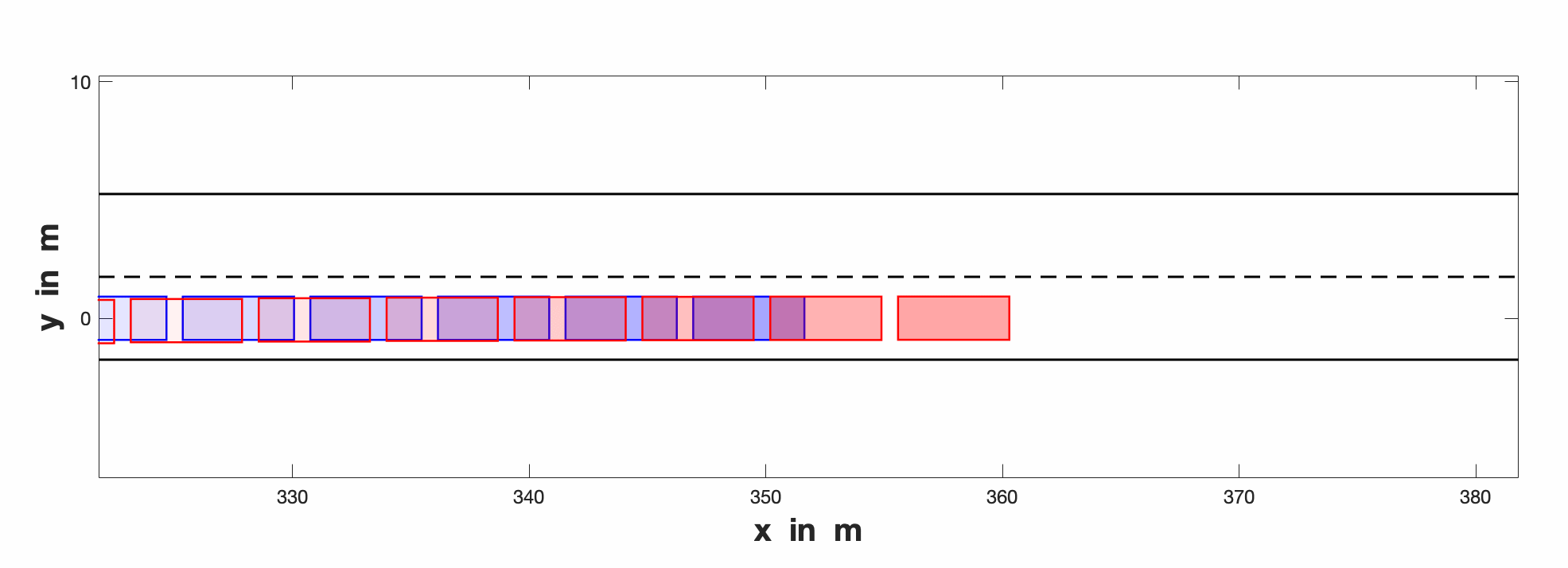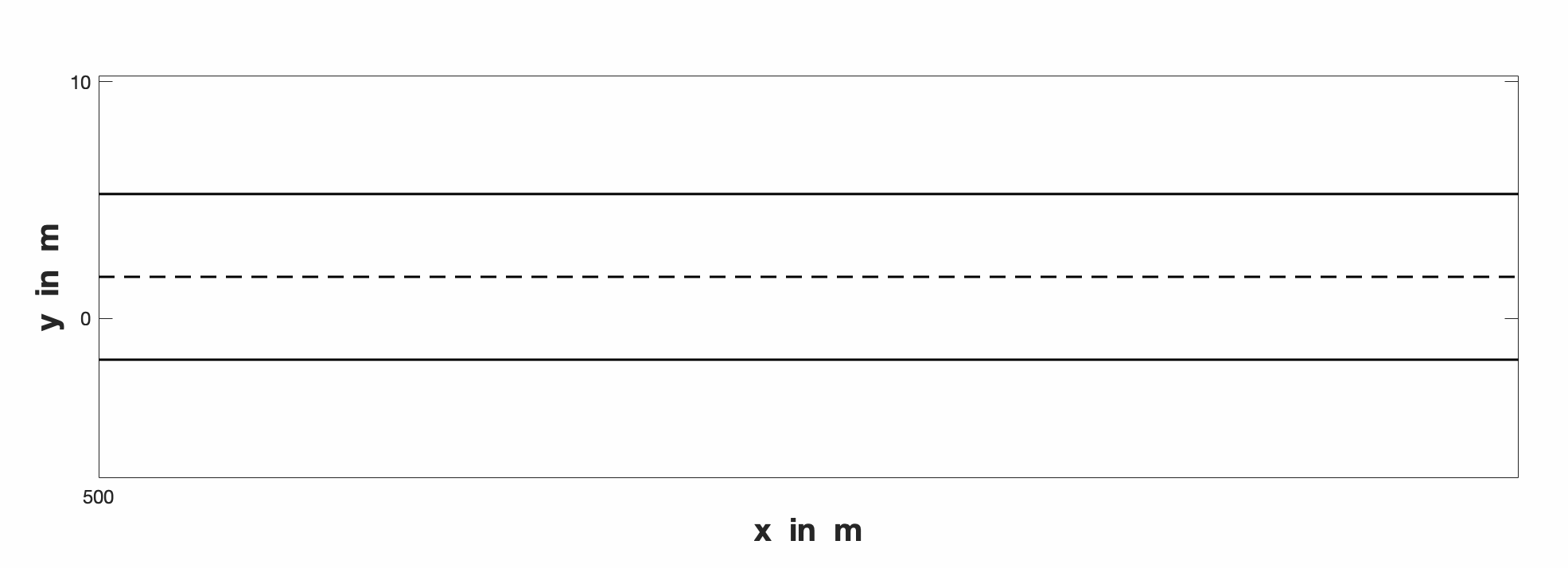
Where red designates ego vehicle that attempts to make lane change and interacting agent blue reacted.